출처: 프로그래머스 코딩 테스트 연습
https://school.programmers.co.kr/learn/courses/30/lessons/62048


나의 풀이
public long solution(int w, int h)
{
long answer = 0;
int gcd = GCD(w, h);
int width = w / gcd;
int height = h / gcd;
double slope = height / (double)width;
for(int x = 0; x < width; ++x)
{
int curY = (int)Math.Floor(slope * x);
int nextY = (int)Math.Ceiling(slope * (x + 1));
answer += (h - (nextY - curY));
}
return answer * gcd;
}
// 공약수가 존재한다면 도형이 합동이다.
private int GCD(int a, int b)
{
if(b == 0) return a;
return GCD(b, a % b);
}최소 공약수를 기준으로 합동으로 보고, 유클리드 호제법으로 공약수를 먼저 구한 다음
해당 구간의 Y값을 기준으로 자른 개수로 남은 사각형을 구하고,
한 합동의 남은 사각형을 구하면 그냥 최대공약수를 곱하면 되는 문제.
유니티에서는 Mathf.Ceil 인데, .Net에서는 Math.Ceilling로 함수 이름이 다르니 주의.
일단 나는 이렇게 풀었는데, 격자에서 직선이 지나는 사각형을 구하는 수학공식이 있다고 한다.
다른 사람 풀이
class Solution {
public long solution(long w,long h) {
long lgcd = gcd(w, h);
long answer = w * h - (w + h - lgcd);
return answer;
}
public long gcd(long a, long b) {
if (b == 0) {
return (long)a;
}
return gcd(b, a%b);
}
}격자를 지나는 대각선이 있을 때, 대각선이 지나는 사각형의 개수는
최소공배수가 없을 때, 가로 + 세로 - 1
최소공배수가 있을 때, 가로 + 세로 - 최소공배수
라는 공식이다.
초등학교 ~ 중학교 저학년에서는
여러 종류의 격자를 그려보면서 귀납적 추론 (a, b, c, d... 였으니까 이런 규칙이구나)으로 설명하고
중학교 고학년에서는 별도 증명을 한다고 한다.
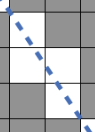
우선 직사각형이 주어질 때,
x의 경우의 수를 구해보자.
x = 1 일 때, y는 3 / 2 => (1, 3 / 2)
x = 2 일 때, y는 3 => (2, 3)

이제 y의 경우의 수를 구해보자
y는 1, 2, 3의 값을 가질 수 있다.

이제 겹치는 점을 제외해야 한다.
직선 위의 점이기 때문에 y가 같으면 x가 같다.
x를 사용해서 구한 y들의 집합과, 나올 수 있는 y의 집합을 중복제거한다.
5개 중 1개가 겹쳐서 점은 4개다.
(사실 최소공배수가 존재하지 않는 서로소 관계면 교점을 지나지 않기 때문에 언제나 마지막 점만 겹쳐서 -1로 일반화할 수 있다.)

각 점은 바로 직전에 있는 네모와 한 개씩 대응되기 때문에
가로(2) + 세로(3) - 중복(1) = 4이다.
최소 공배수가 존재하는 경우
합동인 도형을 한번 구한 다음 * 최소공배수를 해주면 된다.
때문에 ((가로 / 최소공배수) + (세로/ 최소공배수) - 1) * 최소공배수.이며,
괄호를 풀어보면 가로 + 세로 - 최소공배수 공식이 나오게 된다.
만약 이 공식을 외워서 풀었다면 Lv2가 아닐테니 기울기로 푸는게 맞을 듯.
(사실 기울기로 따져도 어려운 문제는 아니다)
'🛡️ 코딩테스트 > 🛡️ 코테 : 프로그래머스' 카테고리의 다른 글
| C# 점 찍기 - 완전탐색 / 프로그래머스 [Lv.2] (0) | 2023.03.26 |
|---|---|
| C# 공원 산책 - 반복문 / 프로그래머스 [Lv.1] (0) | 2023.03.25 |
| C# 거리두기 확인하기 - 완전탐색DFS / 프로그래머스 [Lv.2] (0) | 2023.03.23 |
| C# 전력망을 둘로 나누기 - 완전탐색DFS / 프로그래머스 [Lv.2] (0) | 2023.03.22 |
| C# 배달 - 다익스트라 / 프로그래머스 [Lv.2] (0) | 2023.03.21 |